Sample Size
By Elisabetta Tola / 3 minute read
One of the drivers of statistical confidence is the size of the study group, also known as the sample size. Rarely do we have perfect data on a complete population. The U.S. census is an attempt to do just that — count every single person in the United States every 10 years.
In terms of data, you can think of it this way: imagine there are 100 people on an island, and you would like to determine their average height. If you measure all 100 people, you would have no margin of error and a 100% confidence level. Your calculation would be exactly right.
But, such situations are rare. More common are sample groups that stand in for an entire population. In our island example, we could sample the heights of 20 people chosen at random in order to estimate the average height of the population. We would probably be close to, but not quite match, the true average height. The larger the sample size, the better the estimate. The smaller the sample, the greater the margin of error and the lower the confidence interval.
Scientific experiments are usually done through random sampling. In statistical terms, a random sample is designed to be representative of the entire population under observation. You may be familiar with this concept in election polls. A similar approach is used in drug testing or in describing biological characteristics from a subgroup of individuals.
Observations vs. Experiments
Observational studies are studies in which the variables and the data are not controlled and are not collected directly by the scientists performing the test. Typically, these studies apply statistical models to data compiled by other public or private entities. Their value is that they can provide insight into the real world instead of in a controlled environment.
Experimental studies provide data that are collected directly by the scientists who analyze them. They can be randomized or not, with or without a control group. For instance, the typical clinical trial is usually a randomized controlled one. Experimental studies make it easier for researchers to control variables and reduce statistical uncertainty, known as “noise.”
Conversely, nonrandom samples, such as groups of volunteers, say nothing about the population as a whole. Therefore, studies that consist of such samples should be viewed with skepticism.
However, sometimes even well-designed samples might turn out to be skewed. It happens when there are either a high number of nonrespondents or a subgroup that inaccurately reports data. For example, a group of people who report on their food intake might truly be a random sample, but their self-reporting could be flawed to the point of making the data irrelevant.
The number of people in the sample matters, too. Small samples are more easily skewed by outliers and more likely to be affected by random errors.
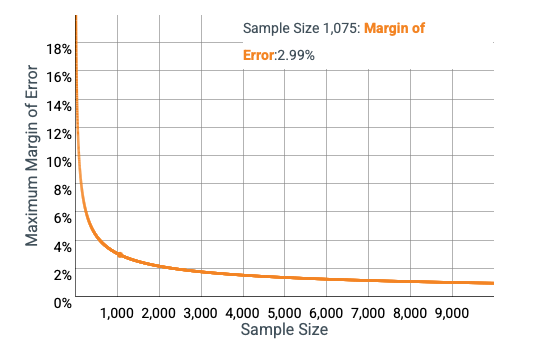
Moreover, as John Allen Paulos writes in A Mathematician Reads the Newspaper, “what’s critical about a random sample is its absolute size, not its percentage of the population.” It might seem counterintuitive, but a random sample of 500 people taken from the entire U.S. population is generally far more predictive — has a smaller margin of error, in other words — than a random sample of 50 taken from a population of 2,500. Different variables, including population size, determine a sample’s reliability. For example, as a rule of thumb, the Italian National Institute of Statistics uses samples of 1,500 to 2,000 people to make periodic surveys of populations, regardless of the overall population.
However, there is an important caveat to sample size: as the British physician and science writer Ben Goldacre points out in The Guardian, small (but still meaningful) effects are difficult to measure in small sample populations.


